Dynamic Programming: Examples, Common Problems, and Solutions

blognet   Saturday, January 30, 2021   How to, Make it Useful   Comment  

There’s no doubt that dynamic programming problems can be very intimidating in a coding interview. Even when you may know that a problem needs to be solved using a dynamic programming method, it’s a challenge to be able to come up with a working solution in a limited time frame.

The best way to be good at dynamic programming problems is to go through as many of them as you can. While you don’t necessarily need to memorize the solution to every problem, it’s good to have an idea of how to go about implementing one.

What Is Dynamic Programming?

Simply put, dynamic programming is an optimization method for recursive algorithms, most of which are used to solve computing or mathematical problems.

You can also call it an algorithmic technique for solving an optimization problem by breaking it into simpler sub-problems. A key principle that dynamic programming is based on is that the optimal solution to a problem depends on the solutions to its sub-problems.

Wherever we see a recursive solution that has repeated calls for the same inputs, we can optimize it using dynamic programming. The idea is to simply store the results of subproblems so that we do not have to re-compute them when needed later.

Dynamically programmed solutions have a polynomial complexity which assures a much faster running time than other techniques like recursion or backtracking. In most cases, dynamic programming reduces time complexities, also known as big-O, from exponential to polynomial.

Now that you have a good idea of what dynamic programming is, it’s time to check out a few common problems and their solutions.

Dynamic Programming Problems

1. Knapsack Problem

Problem Statement

Given a set of items, each with a weight and a value, determine the number of each item to include in a collection so that the total weight doesn’t exceed a given limit and the total value is as large as possible.

You’re given two integer arrays values[0..n-1] and weights[0..n-1] which represent values and weights associated with n items respectively. Also given is an integer W which represents the knapsack capacity.

Here we’re solving the 0/1 knapsack problem, which means that we can choose to either add an item or exclude it.

Algorithm

• Create a two-dimensional array with n+1 rows and w+1 columns. A row number n denotes the set of items from 1 to i, and a column number w denotes the maximum carrying capacity of the bag.
• The numeric value at [i][j] denotes the total value of items up till i in a bag that can carry a maximum weight of j.
• At every coordinate [i][j] in the array, pick the maximum value that we can obtain without item i, or the maximum value that we can obtain with item i---whichever is larger.
• The maximum obtainable value by including item i is the sum of item i itself and the maximum value that can be obtained with the remaining capacity of the knapsack.
• Perform this step until you find the maximum value for the W^th row.

Code

def FindMax(W, n, values, weights):
    MaxVals = [[0 for x in range(W + 1)] for x in range(n + 1)]
 
    for i in range(n + 1):
        for w in range(W + 1):
            if i == 0 or w == 0:
                MaxVals[i][w] = 0
            elif weights[i-1] <= w:
                MaxVals[i][w] = max(values[i-1]
                          + MaxVals[i-1][w-weights[i-1]],  
                              MaxVals[i-1][w])
            else:
                MaxVals[i][w] = MaxVals[i-1][w]
 
    return MaxVals[n][W]

2. Coin Change Problem

Problem Statement

Suppose you’re given an array of numbers that represent the values of each coin. Given a specific amount, find the minimum number of coins that are needed to make that amount.

Algorithm

• Initialize an array of size n+1, where n is the amount. Initialize the value of every index i in the array to be equal to the amount. This denotes the maximum number of coins (using coins of denomination 1) required to make up that amount.
• Since there is no denomination for 0, initialise the base case where array[0] = 0.
• For every other index i, we compare the value in it (which is initially set to n+1) with the value array[i-k] +1, where k is less than i. This essentially checks the entire array up till i-1 to find the minimum possible number of coins we can use.
• If the value at any array[i-k] + 1 is lesser than the existing value at array[i], replace the value at array[i] with the one at array[i-k] +1.

Code

def coin_change(d, amount, k):
    numbers = [0]*(amount+1)
 
    for j in range(1, amount+1):
        minimum = amount
        for i in range(1, k+1):
            if(j >= d[i]):
                minimum = min(minimum, 1 + numbers[j-d[i]])
            numbers[j] = minimum
 
    return numbers[amount]

3. Fibonacci

Problem Statement

The Fibonacci Series is a sequence of integers where the next integer in the series is the sum of the previous two.

It’s defined by the following recursive relation: F(0) = 0, F(n) = F(n-1) + F(n-2), where F(n) is the n^th term. In this problem, we have to generate all the numbers in a Fibonacci sequence up till a given n^th term.

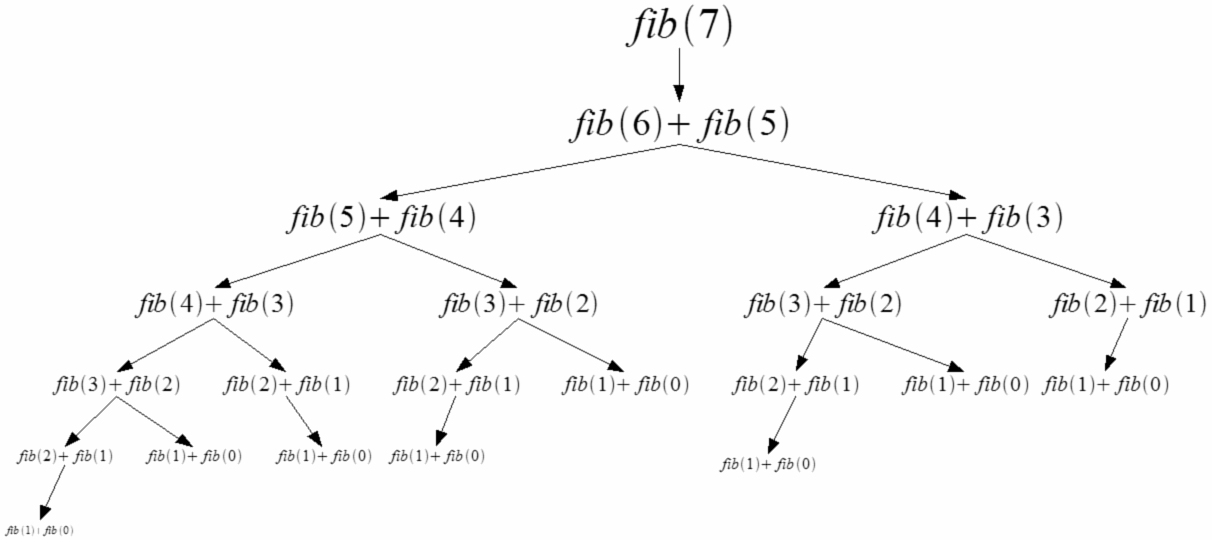
Algorithm

• First, use a recursive approach to implement the given recurrence relation.
• Recursively solving this problem entails breaking down F(n) into F(n-1) + F(n-2), and then calling the function with F(n-1) and F(n+2) as parameters. We do this until the base cases where n = 0, or n = 1 are reached.
• Now, we use a technique called memoization. Store the results of all function calls in an array. This will ensure that for every n, F(n) only needs to be calculated once.
• For any subsequent calculations, its value can simply be retrieved from the array in constant time.

Code

def fibonacci(n): 
    fibNums = [0, 1] 
    for i in range(2, n+1):
        fibNums.append(fibNums[i-1] + fibNums[i-2])
    return fibNums[n] 

4. Longest Increasing Subsequence

Problem Statement

Find the length of the longest increasing subsequence inside a given array. The longest increasing subsequence is a subsequence within an array of numbers with an increasing order. The numbers within the subsequence have to be unique and in ascending order.

Also, the items of the sequence do not need to be consecutive.

Algorithm

• Start with a recursive approach where you calculate the value of the longest increasing subsequence of every possible subarray from index zero to index i, where i is lesser than or equal to the size of the array.
• To turn this method into a dynamic one, create an array to store the value for every subsequence. Initialise all the values of this array to 0.
• Every index i of this array corresponds to the length of the longest increasing subsequence for a subarray of size i.
• Now, for every recursive call of findLIS(arr, n), check the n^th index of the array. If this value is 0, then calculate the value using the method in the first step and store it at the n^th index.
• Finally, return the maximum value from the array. This is the length of the longest increasing subsequence of a given size n.

Code

def findLIS(myArray):
    n = len(myArray)
    lis = [0]*n
 
      for i in range (1 , n):
        for j in range(0 , i):
            if myArray[i] > myArray[j] and lis[i]< lis[j] + 1 :
                lis[i] = lis[j]+1
  
    maxVal= 0
    for i in range(n):
        maxVal = max(maxVal , lis[i])
  
    return maxVal

Solutions to Dynamic Programming Problems

Now that you’ve gone through some of the most popular dynamic programming problems, it’s time to try implementing the solutions by yourself. If you’re stuck, you can always come back and refer to the algorithm section for each problem above.

Given how popular techniques such as recursion and dynamic programming are today, it won’t hurt to check out some popular platforms where you can learn such concepts and hone your coding skills. While you might not run into these problems on a daily basis, you'll surely encounter them in a technical interview.

Naturally, having the know-how of common problems is bound to pay dividends when you go for your next interview. So open up your favourite IDE, and get started!