Excel is a powerful tool, particularly so for financial analysts and accountants. Whether you’re a research analyst, an investment banker, or just someone trying to build a DCF model, you’ll find these formulas helpful.
1. PMT
Formula: =PMT (rate, nper, pv, [fv], [type])Rate: Rate of interest accruing each period.
NPER: Total number of payments.
PV: Amount of loan or the present value of all payments.
[fv]: This is an optional argument where you may input a target balance of cash you’d like after the loan has been repaid; it is set to 0 by default.
[type]: This is an optional argument where you can choose to make payments due at the beginning (1) or the end of the period (0); it is set to 0 by default.
The PMT function allows real estate analysts to build a financial model to compute the periodic payments to pay off the principal within a given term. However, you may use the function for any type of loan.
Therefore, the analysts will need the principal amount, interest rate, and the frequency of payments. For instance, the following is an example of a $200,000 loan accruing interest at 6% with a 5-year term.
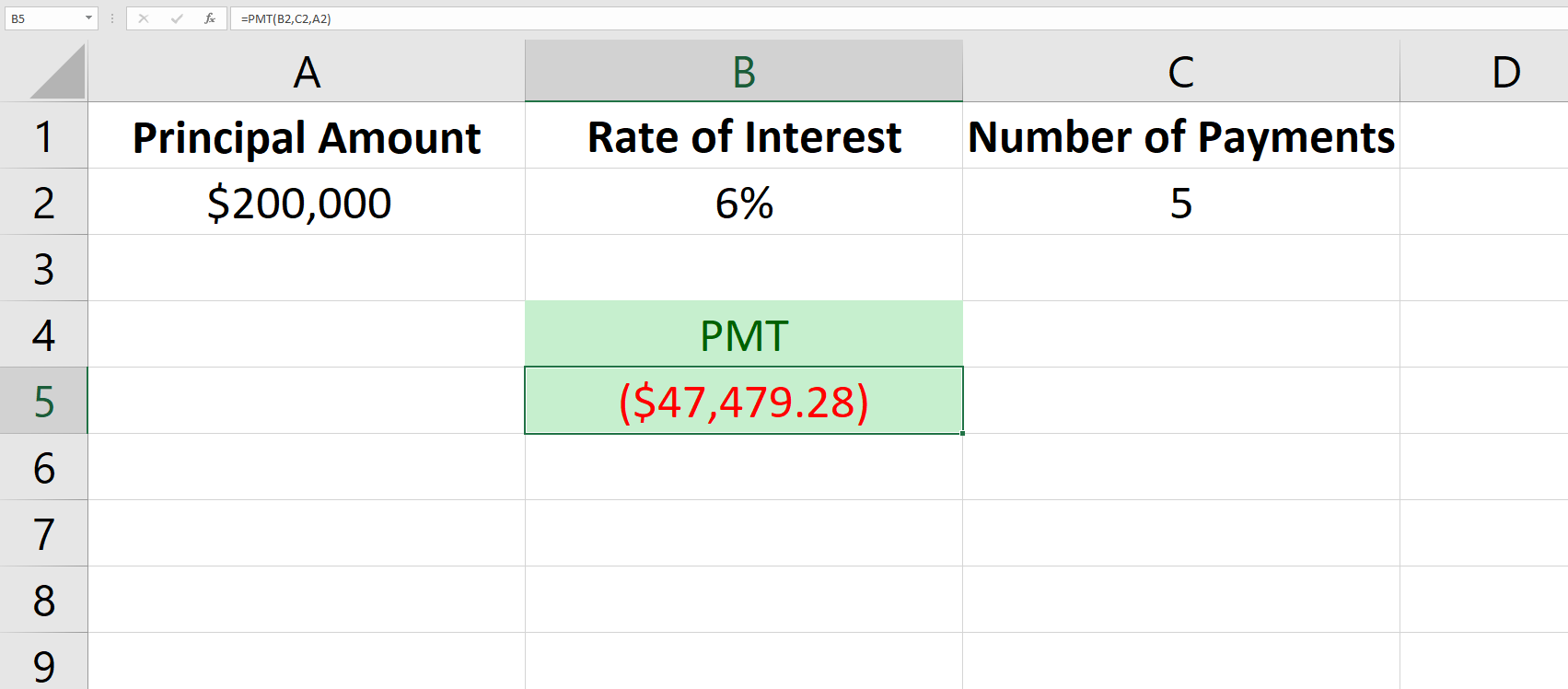
This tells the analyst that this $200,000 loan that accrues interest annually at the rate of 6% will require an annual payment of $47,479.28 for 5 years to pay off the loan (i.e., principal plus interest).
Here, it's important to note that if interest accrues monthly, the effective interest rate changes. That will be revealed in the following formula.
2. EFFECT
Formula: =EFFECT (nominal_rate, npery)Nominal_rate: The stated interest rate.
Npery: Number of times the interest will compound per year.
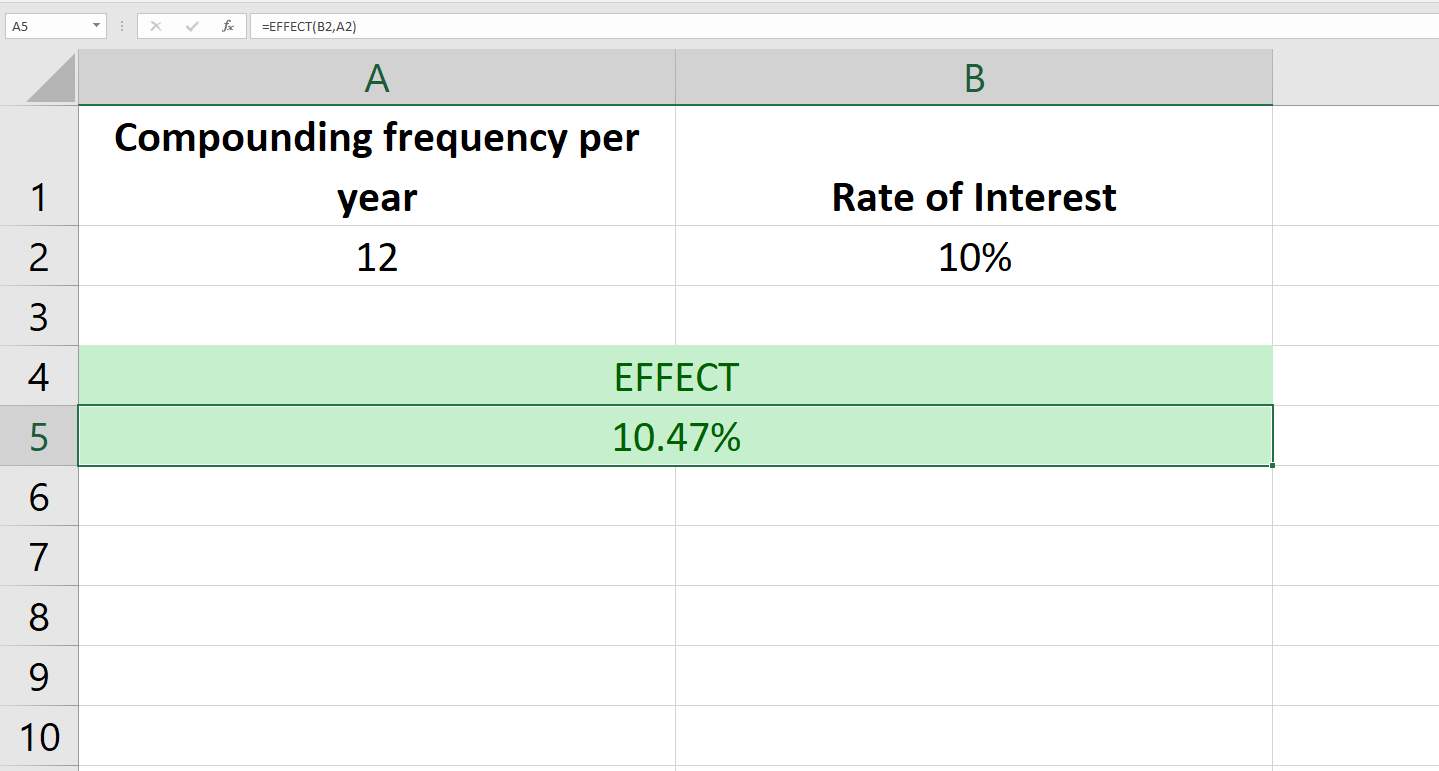
The EFFECT function computes the effective interest rate. For instance, when an interest rate is stated as 10% compounded monthly, the effective rate will be higher than 10%. Here’s an example showing this computation with the EFFECT function.
3. XNPV
Formula: =XNPV (rate, values, dates)Rate: The rate at which you’d like to discount the cash flows.
Values: Cell range containing the cash flows.
Dates: The dates corresponding to the cash flows.
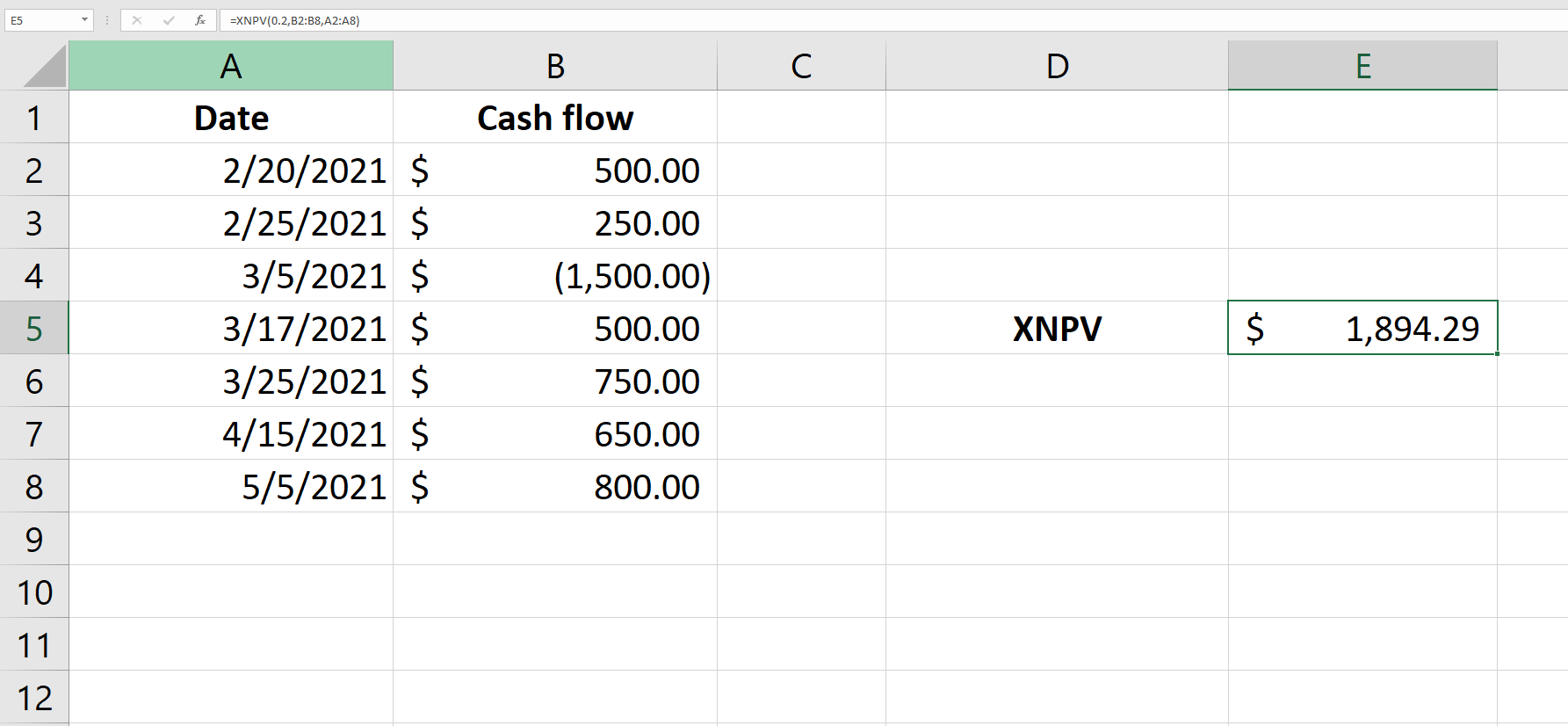
XNPV is a variation in the NPV (net present value). Therefore, you can use XNPV to compute the net present value as well. However, the difference is that XNPV doesn’t assume that the cash flows occur at equal time intervals.
When using the XNPV formula, remember that the rate argument must always be supplied as a percentage (i.e., 0.20 for 20%). You should use a negative value for payments, and a positive value for receipts.
The cells containing the dates must be formatted as a date and not as text. Also, note that the data must be arranged in chronological order.
4. XIRR
Formula: =XIRR (values, dates, [guess])Values: Cell references to cells containing cash flows.
Dates: The dates corresponding to the cash flows.
Guess: An optional argument where you can input an expected IRR; it’s set to 0.1 by default.
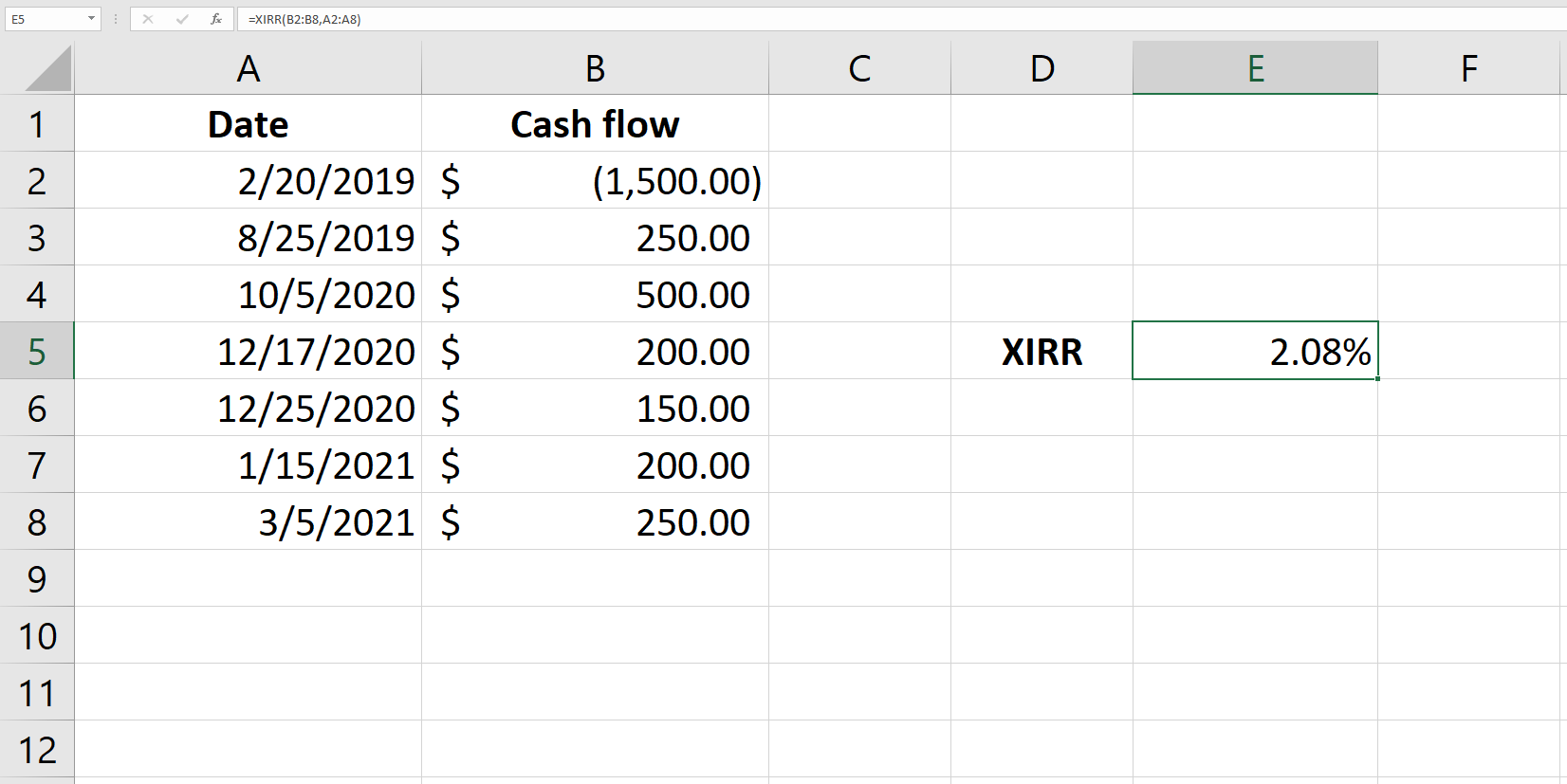
XIRR stands for Extended Internal Rate of Return. Much the same way as XNPV, the only difference here is that XIRR doesn’t assume that the cash flows occur at regular intervals.
If you’re wondering why Excel requires you to input a guess, it’s because the XIRR is calculated through iterations. If you provide a guess, the iterations start from that number, or 0.1 otherwise.
If Excel fails to calculate a rate after a certain number of iterations, it returns a #NUM error. Excel will also return a #NUM error if the data doesn’t have at least one negative and one positive cash flow.
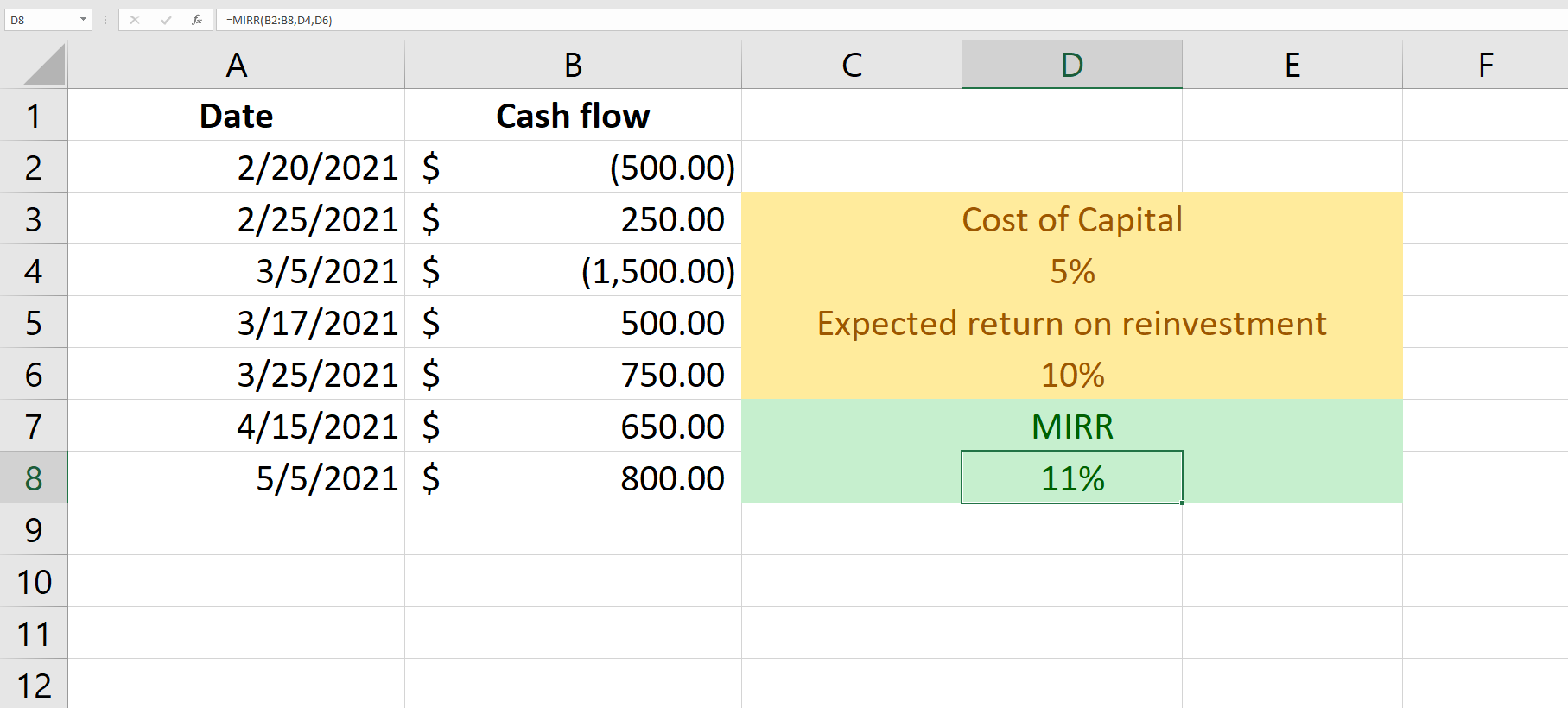
5. MIRR
Formula: =MIRR (values, finance_rate, reinvest_rate)Values: Cell references to cells containing cash flows.
Finance_rate: Cost of capital.
Reinvest_rate: Expected rate of return on reinvested cash flows.
According to the XIRR, the positive cash flows are reinvested at the IRR. However, the modified internal rate of return (MIRR) assumes that they're invested at the company's cost of capital or the external rate of return.
Unlike the XIRR function, MIRR does assume that the cash flows occur periodically. However, many of the other conditions remain the same. You must have at least one positive and negative cash flow in the data and the values should be in chronological order.
6. RATE
Formula: =RATE (nper, pmt, pv, [fv], [type], [guess])NPER: Total number of payments until maturity.
PMT: Amount of payment each period.
PV: Present value of the payments across the life of the bond, i.e., the cost of the bond.
[fv]: This is an optional argument that you can set to the desired balance of cash after the final payment; it’s set to 0 by default.
[type]: This is an optional argument to set the payment as due at the end (0) or beginning (1) of the period; it’s set to 0 by default.
[guess]: This is an optional argument where you can input a guessed rate; it’s set to 0.1 by default.
The RATE function allows analysts to calculate a bond’s Yield to Maturity. The function uses iterations for computation, and if the results don’t converge by the 20th iteration, it will return a #NUM error.
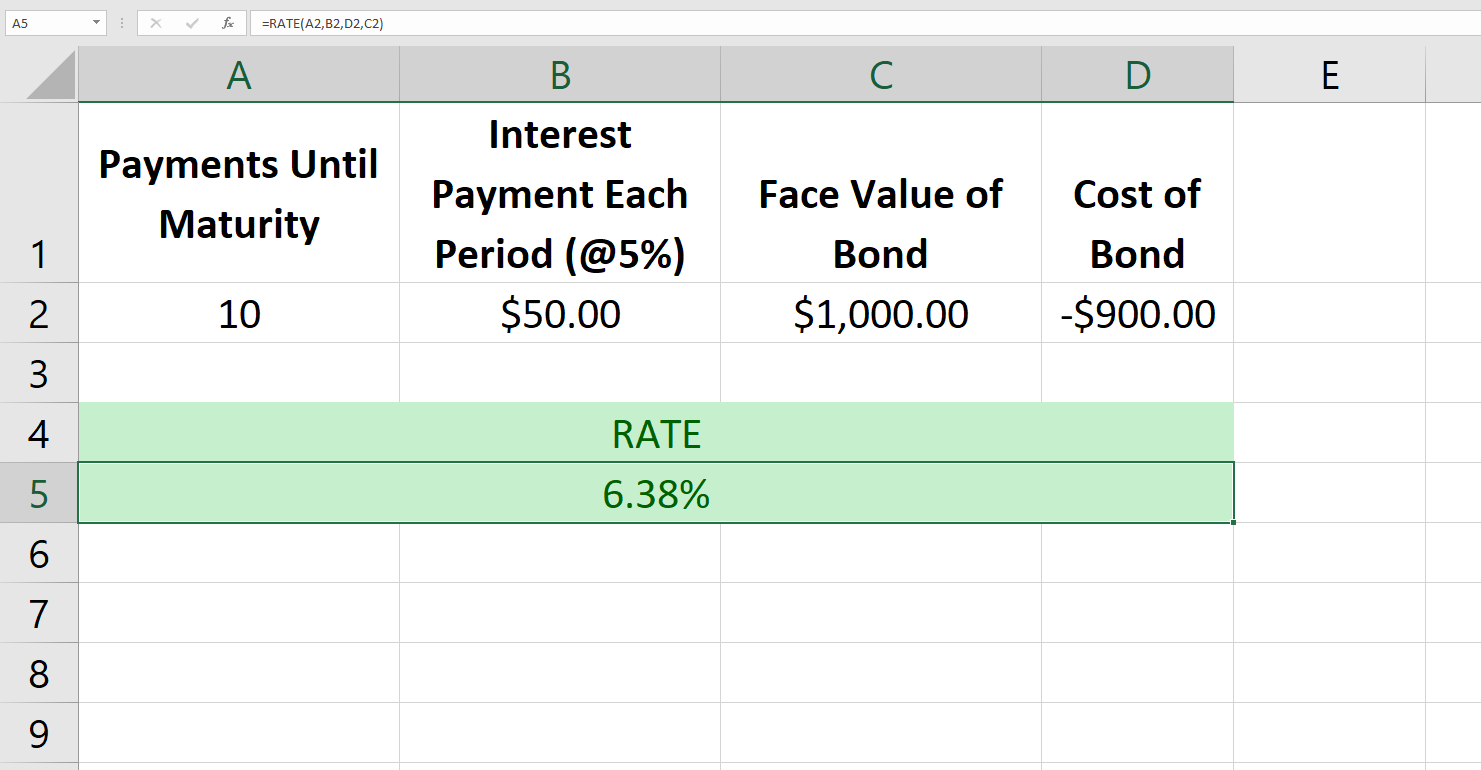
Note that the cost of the bond must be a negative number, otherwise, the function will return a #NUM error.
7. SLOPE
Formula: =SLOPE (known_ys, known_xs)Known_ys: A cell range or an array consisting of the dependent variable data points.
Known_xs: A cell range or an array consisting of the independent variable data points.
The SLOPE function computes the slope of a regression line, also known as the line of best fit. This is a handy tool when you want to compute a stock’s beta using a data set containing the prices of a stock and daily index levels.
Following is an example of how you can compute the slope of a regression line with the SLOPE function.
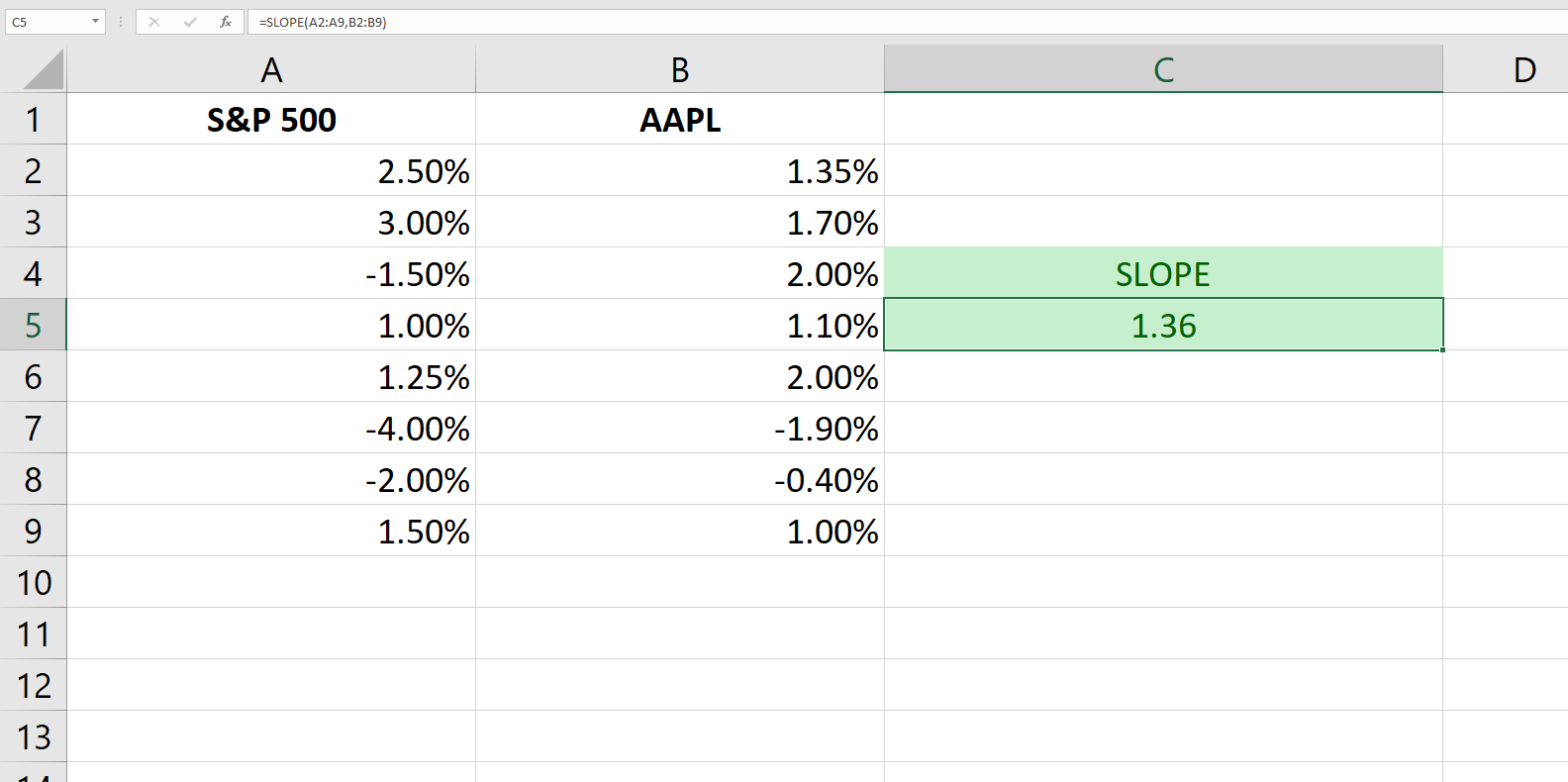
If you supply only one dependent and independent data point, the function will return a #DIV/0 error. If the ranges you enter in each argument don’t have an equal number of data points, the function will return a #N/A error.
You’re Now Ready With Your Financial Formulas Toolkit
Financial modeling can be a dizzying experience with numbers floating across your screen. These Excel finance functions will make your life a little easier so you don’t have to use long, complex formulas to make your computations. These functions, though, may not be able to help you do your taxes.